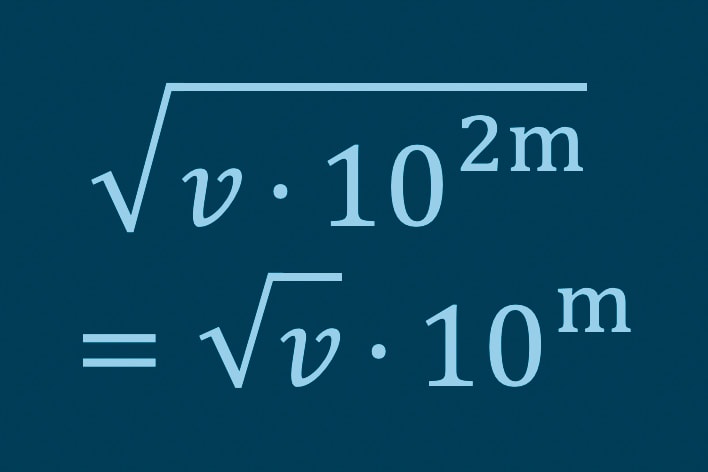Arbitrary Precision Square Root in JavaScript

I've recently been working on a square root function for my arbitrary precision floating-point numbers used in Very Plotter, my JavaScript explorer for the Mandelbrot set among other things.

JavaScript has a built-in BigInt type. This allows performing math operations on integers of arbitrary size, but there is no built-in BigInt square root function.

First I'll show my floating-point numbers that are built using of this BigInt type, and then I'll explain my square root algorithm.

Floating-point Numbers with BigInt

Since BigInt values are integers, we can represent a decimal value using two BigInt values: a mantissa (here called v) and exponent (e). I am using a power of 10 for the exponent e value. For example, the value "123.456" can be represented as:

$$123.456=\mathrm{123,456}\cdot {\mathrm{10}}^{-3}$$

which looks like this as JavaScript object (with literal n-suffixed BigInt values):

{
  v: 123456n,
  e: -3n
}

And where integers are just $v\cdot {10}^0$, for example 789:

{
  v: 789n,
  e: 0n
}

Since BigInt values can be of arbitrary size, we can precisely represent the decimal value 0.7436439270580283166312913614158260087397027582242801496395455597668233520653387568335095347658086878861866587992249385555025719 with two BigInt integers as follows:

{
  v: 7436439270580283166312913614158260087397027582242801496395455597668233520653387568335095347658086878861866587992249385555025719n,
  e: -127n
}

Dealing with the Exponent During the Square Root

Our values:

$$v\cdot {10}^e$$

can be slightly adjusted to take the form:

$$v\cdot {10}^{\mathrm{2m}}$$

for which the square root can be simply expressed as:

$$\sqrt{v\cdot {10}^{\mathrm{2m}}}=\sqrt{v}\cdot {\mathrm{10}}^{\mathrm{m}}$$

where we halve our exponent e value and take the square root of the v value.

If we have an odd e value, we cannot simply halve it (since BigInt values must be integers). Instead, we just have to multiply the v by 10 and reduce the e value by 1 (making e an even number) before taking the square root:

$$v\cdot {10}^e=10v\cdot {10}^{e-1}$$

Finding the Square Root

Now that we know how to deal with the exponent e, we can worry about the square root of our mantissa v.

To compute that, we will use Heron's Method with a starting guess (we'll call $g$) computed with JavaScript's built-in Math.sqrt().

Summarizing the above-linked section of the Wikipedia article, Heron's method works as follows to take the square root of a value $v$:

If our guess $g$ is correct, then $g\cdot g=v$. Therefore:

If our guess $g$ is an under estimate (too small), then $\frac{v}{g}$ will be an over estimate.

And if our guess $g$ is an over estimate (too large), then $\frac{v}{g}$ will be an under estimate.

Either way, we can get closer to the actual value by taking the average of those:

$$\frac{g+\frac{v}{g}}{2}$$

This process is repeated until our guess $g$ stops changing or only differs by $\pm 1$ from its previous value.

Although division is itself likely a slow precision-losing operation for BigInt values, since we are dividing by $2$ for one of these divisions we can simply perform a right bitwise shift instead with >> 1n.

Our Initial Guess

We can convert a low-precision approximation our BigInt value v into a regular JavaScript number, and use the built-in Math.sqrt() function to get a low-precision (but very good!) approximation of the square root.

To get this approximation, we'll effectively convert the least-significant digits to zeroes and use the above exponent halving rule again. For example, to get an approximation of the square root for the value 131825980877906947146424:

$$13182598087790694714642\cong$$ $$13182598087790690000000$$

which can be expressed as:

$$13182598087790690000000=$$ $$1318259808779069\cdot {10}^7=$$ $$10\cdot 1318259808779069\cdot {10}^6$$

Therefore, its square root can be expressed as:

$$\sqrt{13182598087790690000000}=$$ $$\sqrt{10\cdot 1318259808779069\cdot {10}^6}=$$ $$\sqrt{13182598087790690}\cdot {10}^3$$

JavaScript floating-point numbers can represent about 17 decimal digits' worth of precision, so the above approximation initially used the most significant 16 digits (reserving one digit in case the exponent is odd). Since the exponent $7$ was in fact odd, we applied the same rule as above in multiplying the value by $10$ and reducing the exponent power by $1$, bringing us to the full 17 decimal digits that can be represented by a JavaScript floating-point number.

From there, we can use JavaScript's Math.sqrt() to get our approximation:

$$\sqrt{13182598087790694714642}\cong$$ $$\sqrt{13182598087790690}\cdot {10}^3=$$ $$\mathrm{Math.sqrt(13182598087790690)}\cdot {10}^3$$

Precision and Performance

Unless we're taking the square root of a perfect square, the result will be an irrational number. In this case, the best we can do is use some extra precision to more accurately represent the irrational square root. For example:

$$\sqrt{1234}\cong \mathrm{35.1283361405005916...}$$

Or more famously:

$$\sqrt{2}\cong \mathrm{1.4142135623730950...}$$

To add precision, we need to make the BigInt mantissa value longer, and adjust the exponent accordingly:

$$\mathrm{1,234}\cdot {\mathrm{10}}^0=\mathrm{12,340,000}\cdot {\mathrm{10}}^{-4}$$

Taking the square root of the larger equivalent form uses 4 more digits of precision in the input BigInt and gives us two more digits of precision in the output:

$$\sqrt{\mathrm{1,234}\cdot {\mathrm{10}}^0}\cong 35\cdot {\mathrm{10}}^0$$ $$\sqrt{\mathrm{12,340,000}\cdot {\mathrm{10}}^{-4}}\cong \mathrm{3,512}\cdot {\mathrm{10}}^{-2}$$

So how many more digits of precision do we need? As we use more and more precision, we should get a better and better approximation of the square root, but at the cost of slowing down the computation.

To test this, I used a seeded pseudo random number generator to compute 4 million numbers of varying lengths. I was then able to run those repeatable test values through several different versions of my function, using varying levels of precision. The tests below were run on my M1 Mac mini (using a single performance core, presumably). Where the initial exponent was odd, another digit of precision is added on top of the number of digits listed.

• with 2 additional digits of precision:
  • ~2e-3% average error
  • this required, on average, 1.44 iterations of Heron's method per square root
  • run time of 1.27s (about 22% faster than with 6 digits of precision)
• with 6 additional digits of precision:
  • ~2e-5% average error
  • this required, on average, 1.65 iterations of Heron's method per square root
  • run time of 1.56s
• with 10 additional digits of precision:
  • ~2e-7% average error
  • this required, on average, 1.88 iterations of Heron's method per square root
  • run time of 1.86s (about 18% slower than with 6 digits of precision)
• with 14 additional digits of precision:
  • ~2e-9% average error
  • this required, on average, 2.16 iterations of Heron's method per square root
  • run time of 2.24s (about 42% slower than with 6 digits of precision)
• with 18 additional digits of precision:
  • ~2e-11% average error
  • this required, on average, 2.37 iterations of Heron's method per square root
  • run time of 2.93s (about 88% slower than with 6 digits of precision)
• with 22 additional digits of precision:
  • ~2e-13% average error
  • this required, on average, 2.58 iterations of Heron's method per square root
  • run time of 3.70s (about 237% slower than with 6 digits of precision)

Based on the above testing, the version of the function I am going to use in Very Plotter, at least initially, adds 10 digits of precision to the given value (11 if the exponent is odd). It should be plenty accurate and fast for my purposes, given that it completed 4 million square roots in about 1.86s.

JavaScript Implementation

Here is all of the above, in JavaScript:

function infNumSqrtHerons(a) {
  if (a.v === 0n) {
    return a;
  }
  // we want to keep exponent an integer, so we must
  //   check whether it's even before dividing by 2
  if (a.e % 2n === 0n) {
    return {
      // increase by 10^10, and reduce exponent accordingly
      v: bigIntSqrtHerons(a.v * 10000000000n),
      e: (a.e - 10n) >> 1n
    };
  } else {
    return {
      // increase by 10^11 here, and reduce exponent accordingly
      v: bigIntSqrtHerons(a.v * 100000000000n),
      e: (a.e - 11n) >> 1n
    };
  }
}

function bigIntSqrtHerons(a) {
  if (a < 0n) {
    throw "cannot take square root of negative value";
  }
  const decimalStr = a.toString(10);
  const tenPowerInitial = decimalStr.length - 16;
  const roughFloatInitial = tenPowerInitial <= 0 ?
    Number(a)
    :
    parseFloat(decimalStr.substring(0,16));

  const oddInitialPower = (tenPowerInitial & 1) === 1;
  let tenPower = 0;
  if (tenPowerInitial > 0) {
    tenPower = tenPowerInitial >> 1;
  }
  const roughFloat = (tenPowerInitial > 0 && oddInitialPower) ?
    roughFloatInitial * 10
    :
    roughFloatInitial;

  let nextGuess =
    BigInt(Math.floor(Math.sqrt(roughFloat)))
    *
    (10n ** BigInt(tenPower));
  let currentGuess;
  let guessDiff;
  do {
    currentGuess = nextGuess;
    // average of currentGuess and (a/currentGuess)
    nextGuess = (currentGuess + (a/currentGuess)) >> 1n;
    guessDiff = currentGuess - nextGuess;
  } while (guessDiff > 1n || guessDiff < -1n)

  return nextGuess;
}